In science and engineering we often work with numerical simulations to model real world phenomena. These models are stochastic computer programs that allow sampling from an implicitly given distribution that depends on the parameters of the program. Often, these models don’t allow for an explicit computation of the likelihood of an observation because their inner mechanics are not completely known or the computation is simply intractable. This becomes a problem if one needs to infer certain parameters of the model from observed data. Indeed, conventional methods for maximum likelihood estimation or Bayesian inference are not directly applicable. The scenario is called likelihood-free inference and has been tackled in the past by methods such as approximate Bayesian computation (ABC) or synthetic likelihood, both of which struggle with high-dimensional data. In recent years, research has focused on methods from deep learning to overcome the limitations of existing approaches. In particular, neural networks have been used to approximate
- The posterior distribution of the parameters, e.g. “SPNE” [Pap18F]
- The likelihood function of the model, e.g. SNLE [Pap19S]
- The likelihood-to-evidence ratio, e.g. “SNRE” [Tho20L]
In the ICLR paper [Glo22V] Thomas et al. propose to combine likelihood(-ratio) and posterior estimation into a single framework. The method first samples from the prior on the parameter and trains a likelihood(-ratio) model. The likelihood model is then used to train a posterior model for the parameters. The process is repeated using sampling importance resampling from the posterior model instead of the prior (see image below).
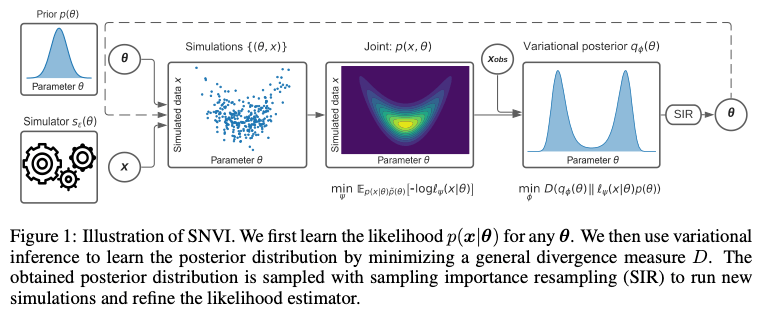
The paper also covers the topic of training loss. Since the emergence of increasingly complex models such as normalizing flows, the question of what is the right divergence to compare the approximated distribution to the real one has become of interest again. Classical backward KL-divergence favors “mode seeking” behavior and can potentially limit the search space to over-simplistic models. In the early days of Variational inference, the posterior models were mostly unimodal and the choice of backward KL-divergence was kind of natural (see e.g. [Ble17V]). With the flexibility that neural approximators offer, one is more interested to capture the entire space of possibilities accurately rather than just the highest mode of the distribution. Another way to look at it is that once we can expect to have a relatively good approximation of the true posterior in our hypothesis space, the question becomes mostly about optimization within this space and the trajectory of our search heavily depends on our choice of loss function. As is shown by the authors, the method is usable with common techniques such as forward KL divergence, importance weighted ELBO [Dom18I], or Renyi alpha-divergences.
The applications are certainly a highlight of the paper. Besides classical benchmarks such as the Lotka-Voltera predator-prey model, there is also a novel application to the pyloric network in the stomatogastric ganglion (STG) of the crab Cancer Borealis, a well-characterized circuit producing rhythmic activity (see image below). In this case the simulator implements a biological neural network, which is somewhat charming.
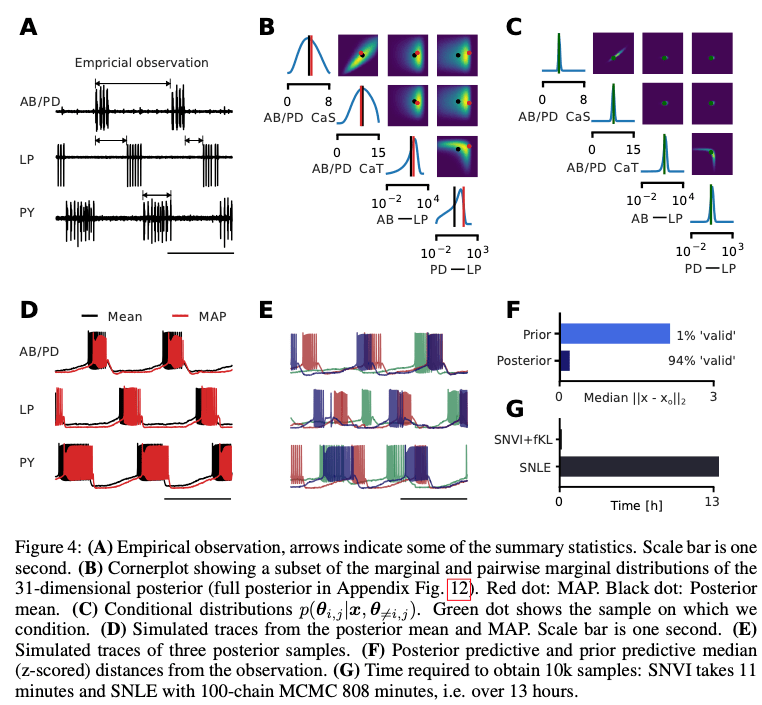
In our engineering projects it is also not uncommon to work with simulators. Good ones are essential for dependent tasks, e.g. when used as environments in RL. Imagine for instance that you are working with a simulator for an airplane, and you would like to tune the simulator’s parameters using data from a real aircraft. This can be a very laborious task requiring lots of expert knowledge and measurements from the real aircraft under controlled conditions. Simulation based inference offers a principled way to automate this expensive task.