Graph neural networks struggle with tasks that rely on long distance interactions between nodes in a graph. This phenomenon is particularly present when GNNs are applied to heterophilic networks and when the neighbourhoods of the nodes grow rapidly with the radius, e.g. exponentially. With an increasing receptive field the GNN is no longer able to encode the information about the entire neighborhood into its representation, a vector of fixed length. For this reason the phenomenon is known by the name (information) over-squashing.
The ICLR 2022 paper [Top22U] aims to provide a precise description of the phenomenon and how it arises from bottlenecks in the graph. They develop an edge based combinatorial notion of curvature - called Balanced Forman curvature - and show that negatively curved edges are responsible for over-squashing.
The definition of the edge-curvature tries to mimic the properties of the Ricci curvature for Riemannian manifolds in the sense that two geodesics - something like a shortest path between two points along a surface - with nearby starting points and “same direction” can either stay parallel (Euclidian space), converge (spherical space) or diverge (hyperbolic space). These local properties can readily be transferred into the graph domain (see image below).
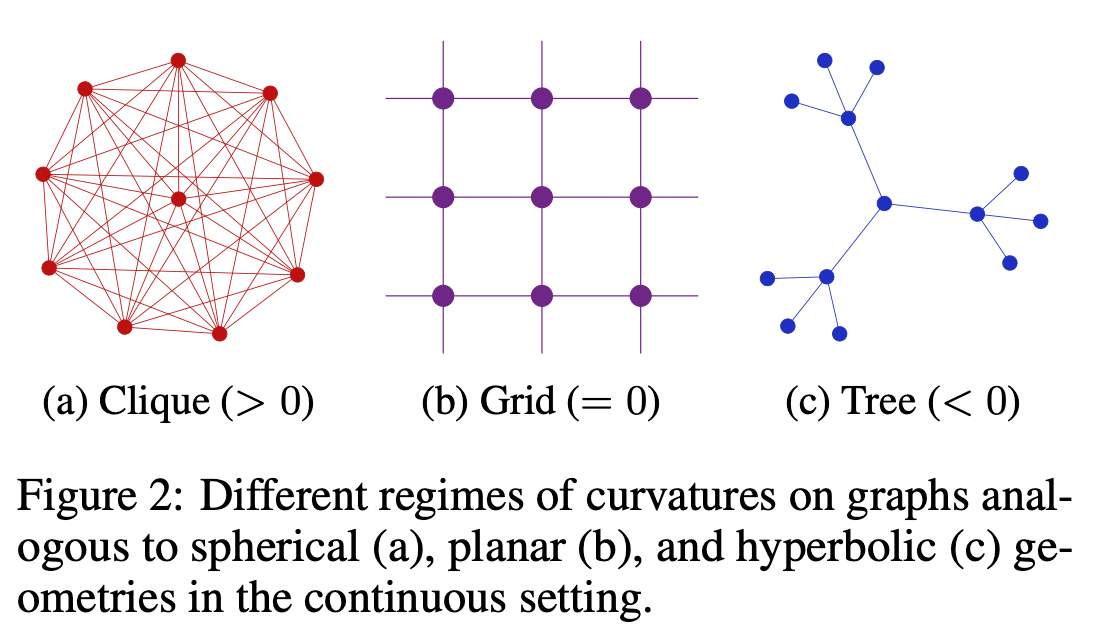
The concept of curvature has previously been transferred to graphs. The most important notions are the “Forman” [For03B] and the “Olivier” curvatures [Oll07R]. While the Forman curvature has a simple combinatorial definition, it is theoretically not well understood. The Olivier curvature has a rich theory but its definition based in optimal transport makes it hard to investigate local properties. The balanced Forman curvature aims to provide the best from both worlds. It poses a relatively simple combinatorial definition based on the number of triangles and (non-triangulated) 4-cycles that start at a certain edge while being a tight lower bound for the Olivier curvature.
The authors show that negatively curved edges with respect to the balanced Forman curvature are responsible for over-squashing in the sense that many nodes in the 2-neighborhood of the endpoints of a sufficiently negatively curved edge have little influence on their representation throughout the computation.
If you know a little about spectral graph theory you might wonder how this is related to the spectral gap and the Cheeger constant of a graph. Intuitively, if the graph can be separated into two sub-communities with very few connections in between, then this should induce over-squashing because all information about the two communities needs to flow over just a few connections. Interestingly, the authors show that the Cheeger constant of a graph can be lower-bounded in terms of half the minimal edge curvature for strictly positively curved graphs. This shows that such communities cannot exist if all edges have positive curvature.
Finally, the authors propose a graph rewiring scheme to eliminate negatively curved edges. They call the procedure Stochastic Discrete Ricci Flow (SDRF). It surgically adds and removes edges in the neighborhood of negatively curved edges in order to alter the local curvature. SDRF preserves the structure of the graph to a much larger extend than previously known rewiring techniques such as DIGL [Gas19D] and proved itself very competitive in the conducted experiment.
With its proper theoretical analysis and the good experimental results this is a pretty solid ICLR publication.