Learning Strides in Convolutional Neural networks
Instead of finding strides through a discrete search, an analogy of the strides hyperparameter for CNNs can be learned during training with gradient descent. The method results in new layer which is based on the discrete Fourier transform, spectral pooling and a “soft mask”.

Strides are an important discrete hyperparameter in convolutional neural networks. Together with pooling layers they control the amount of downsampling happening in the data processing, and changes in them can significantly affect accuracy. Therefore, a costly hyperparameter search for the best strides is often necessary to reach optimal performance of a CNN.

What if we could learn the best strides directly instead of performing a discrete search? [Ria22L] introduces the DiffStride layer that does exactly that - a keras implementation is provided by the authors.

There are two main ideas underlying the new layer:

  1. Instead of reducing the image size through strided convolution followed by pooling, it is done by cropping the discrete Fourier transform (DFT) of the image around its center and transforming back. This operation is a low pass filter, the DFT is differentiable and pooling of this type, called “Spectral Pooling” [Rip15S], has been shown to perform well in CNNs.
  2. While cropping to a fixed size box is non-differentiable (in the size of the box), this cropping can be softened to multiplication with a parametrized, mask-like matrix which is differentiable in the parameter governing its size. This mechanism was put forward in “Adaptive attention span in transformers” [Suk19A] for learning the size of attention context in transformer layers. The soft mask from that paper is shown in the figure. The parameter $z$ determines its size, taking a derivative w.r.t. $z$ results in a non-trivial gradient because of the non-constant profile of the soft mask and thus $z$ can be learned through gradient descent. $R$ becomes a hyperparameter of the neural network.

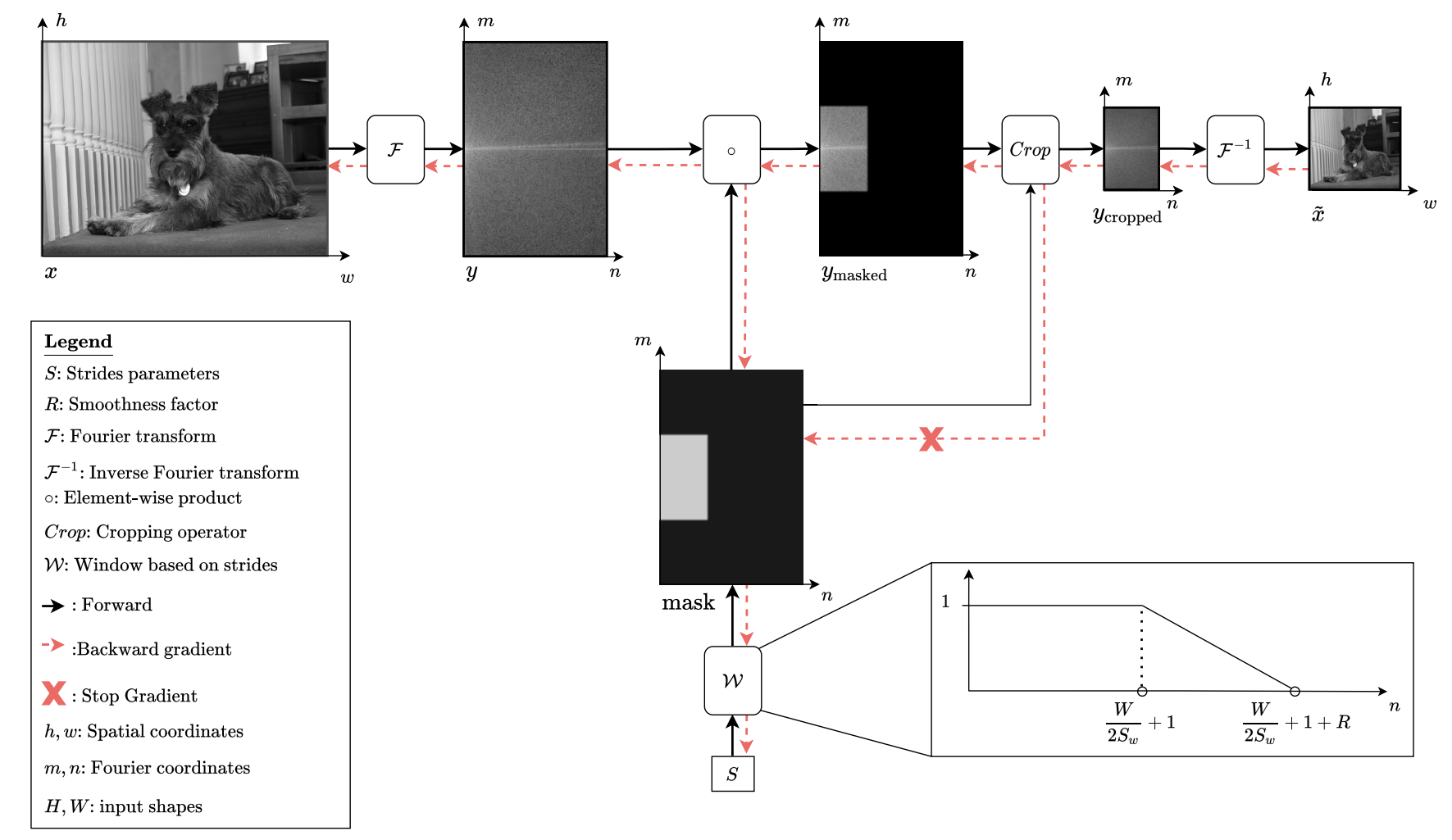
The DiffStride layer is a combination of these ideas - a 2-dimensional soft mask, analogous to the one-dimensional discussed above, is multiplied with the DFT of the input. The height and width of the soft mask can be learned through gradient descent. The region in which the soft mask is zero is cropped (a non-differentiable operation which is performed with stop-grad) and the inverse DFT results in a smaller image. This processing is displayed in the architecture diagram below.

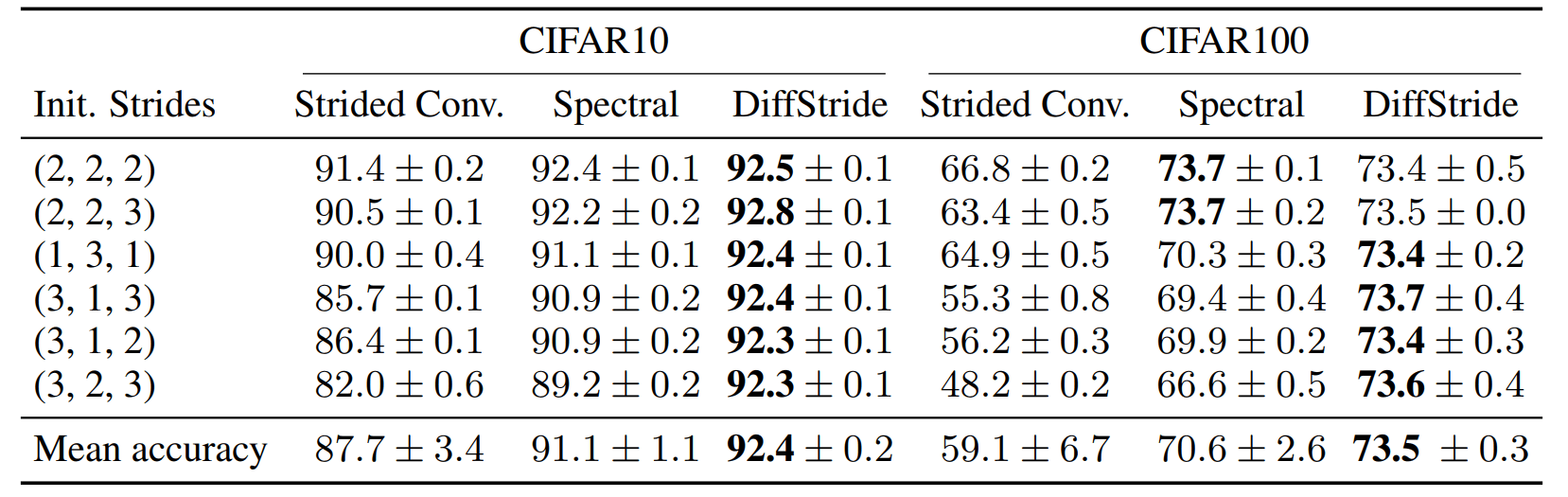
Experiments show that comparable or even slightly better performance to optimal strides (found through discrete search) in a normal Resnet can be reached starting out with random strides and using the new DiffStride layer. This paper is thus a valuable contribution for all practitioners who don’t want to run a hyperparameter search over strides when training a CNN.

References