It is not uncommon that anomaly detection has to be conducted on several time series in parallel. One example are power grids, where sensors are located at different geographic locations. Readings from close-by sensors are often correlated and may be causally related under cascading effects. Bayesian networks are well established as a tool to model such dependencies probabilistically. This allows us to combine generative models for the individual time series into a joint generative model. Such a model can be used to perform anomaly detection jointly for the entire system and therefore hopefully contribute to a more fine-grained analysis.
This is good if we have an idea of how the dependencies between the different time series look like, but what if we don’t know the dependencies? The ICLR paper [Dai22G] by Dai and Chen proposes to learn the dependency graph jointly with the generative model. They use an autoregressive conditional normalising flow to model each time series where the value at time t is conditioned on all previous values itself and all parents in the dependency graph. This conditioning is implemented using a latent representation of the dependencies for each time series. The representation is computed in two stages:
- A representation for each time series’ history is computed by some RNN model
- Starting from the history representation, a dependency representation is obtained by a GNN that passes messages along the edges of the dependency graph
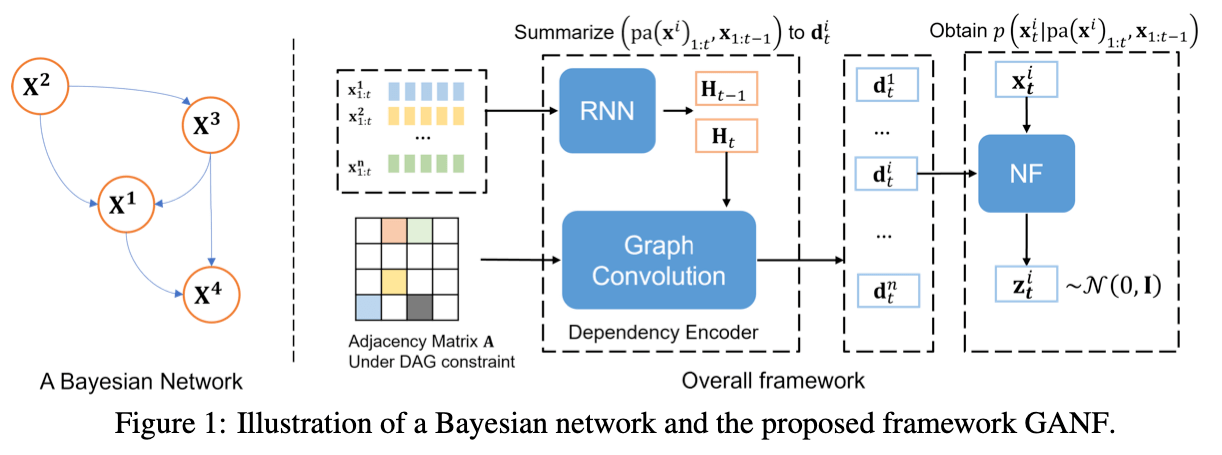
Finally, all components are trained jointly with the adjacency matrix of the dependency graph. The graph is learned via a differentiable loss function, which yields a weighted adjacency matrix, i.e. an edge between $i$ and $j$ exist if the entry at $(i,j)$ is non-zero. To ensure the acyclicity of the graph the authors adopt a technique from [Zhe18D]. The optimization is constrained by an equation that characterises acyclicity, turning the problem into a differentiable one. The resulting constrained optimization problem can then be solved using the augmented Lagrangian method.
I know the problem of anomaly detection on interdependent time series from my own praxis, and I believe that approaches such as the presented one are of great potential to improve the quality of the anomaly detection systems in such cases.