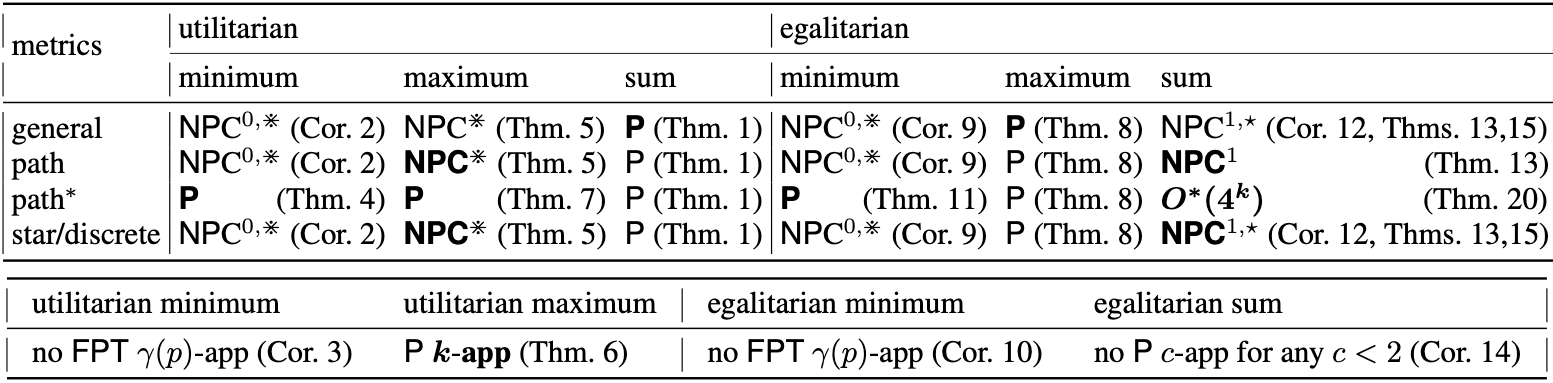
Approval-based multi winner voting is a popular and widely applicable formalism for defining a collective choice of a group based on their individual favorite. The IJCAI 2022 paper [Yan22C] considers the case where the candidates are embedded into a metric space and the unhappiness of a voter with a candidate is proportional to the distance to their favorite candidate. More precisely, the model consists of m candidates, n votes among candidates, and the distances between the candidates. The goal is to select exactly k candidates (k-committee) as winners. The selection rule is based on the metric of the candidates but also depends on the underlying philosophy of the voting system:
- the unhappiness of a voter with a committee might depend on the maximal/minimal/summed distance to their selected candidate
- The voting can be utilitarian (minimizes the summed unhappiness of all voters) or egalitarian (minimizes the maximal unhappiness among the voters)
I think this is a quite reasonable extension which makes this kind of voting schemes applicable to a much wider range of use-cases. As a stylized example one can imagine a travel agency that organizes long distance bus rides dynamically based on the requests through their online system. Customers will likely accept the ride if it will bring them close enough to their destination, but the bus can only stop at k destinations per trip. Hence, the company tries to select k cities such that the summed distance to the true destinations of the customers is as low as possible (utilitarian-minimum).
The paper studies the computational complexity of computing approved winning committees under the aforementioned selection rules. Notably, it provides a relatively complete picture of the complexity landscape, and it turns out that often there is hope to compute good committees. In fact, despite many variants being NP-hard, they show that at least some of them allow efficient approximation algorithms or fixed-parameter tractable algorithms in parameters such as the number of votes, candidates or distinct distances between the candidates. Additionally, they study the complexity on some practically relevant discrete metrics such as star or path metrics.
Complexity of voting schemes